@DFS, 백트래킹 / 3h
예전에 풀었던 문제인데, 처음 풀 때는 진짜 잘 풀었었는데
이번에는 2시간 넘도록 통과도 못했다..ㅠㅠ 계속 틀렸습니다 뜨고 ㅎㅎ
실력이 퇴보한건가..
결국 예전 코드 + 다른 코드를 참고해서 다시 짰다.
문제 링크
https://www.acmicpc.net/problem/15684
15684번: 사다리 조작
사다리 게임은 N개의 세로선과 M개의 가로선으로 이루어져 있다. 인접한 세로선 사이에는 가로선을 놓을 수 있는데, 각각의 세로선마다 가로선을 놓을 수 있는 위치의 개수는 H이고, 모든 세로선이 같은 위치를 갖는다. 아래 그림은 N = 5, H = 6 인 경우의 그림이고, 가로선은 없다. 초록선은 세로선을 나타내고, 초록선과 점선이 교차하는 점은 가로선을 놓을 수 있는 점이다. 가로선은 인접한 두 세로선을 연결해야 한다. 단, 두 가로선이 연속하거나 서로
www.acmicpc.net
사고 흐름
쉬운 설명을 위해 세로선x와 세로선x+1 사이를 '라인'으로 지칭하겠다.
일단 세로선과 가로선들의 교차점들을 배열의 칸으로 잡았다.
그리고 오른쪽에 가로선이 있을 경우 칸에 1을, 왼쪽에 가로선이 있을 경우 -1을 넣어줬다.
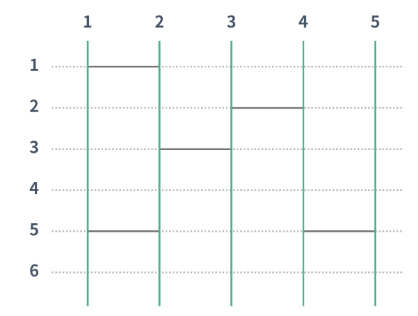
이 경우 맨 왼쪽 맨 위의 가로선의 값은
map[0][0] = 1, map[0][1] = -1로 들어가게 된다.
(0,0)이 세로선 1과 가로선 1의 교차점이다.
1. 한 라인의(세로선 x와 세로선 x+1 사이의 가로선)은 무조건 짝수개여야 한다.
홀수개인 경우 절대로 모든 세로선 i번째에서 시작해서 i번째로 도착할 수 없다.
(물론 짝수개라 해서 다 도착할 수 있는 것도 아니다.)
2. 그래서 각 라인마다 연결된 가로선 개수를 세서
홀수인 것들이 3개를 초과하면 바로 끝나도록 구현했다.
(이것만 해도 시간이 엄청 빨라진다)
3. 그리고 홀수선이 3개 이하인 경우, 이 세로선들에만 조합을 이용해 가로선을 추가해서 사다리가 성립하는지 체크했다.
여기서 망했다. 테케는 다 돌렸지만 제출하면 틀렸습니다가 뜬다.
당연히 그럴 수 밖에 없는게, 한 라인의 가로선 개수가 짝수가 된다고 무조건 i번째출발 → i번째도착 이 성립하지 않는다.
반례가
1) 가로선이 홀수인 라인이 하나인데, 그 라인에 가로선이 세개 필요한 경우
2) 가로선이 다 짝수이지만, 짝수개를 더 추가해야 하는 경우
...
등 수도 없이 많다.
이 생각을 못해서 2시간동안 잘못된 로직으로 고생했다.
4. 결국 이 문제는 완전탐색을 해야 하는 문제다.
사다리 개수가 0개일때, 1개일때, 2개일때, 3개일때 모두!
대신 시간을 획기적으로 줄여줄 수 있는 방법은
1) 위에서 말한 '라인의 가로선이 짝수개여야 한다' 와
2) 가로선을 긋기 전 그을 수 없는 경우를 미리 체크한다
이 두가지이다.
2)의 경우,
if (map[i][j] != 0 || map[i][j + 1] != 0) continue;이렇게 가로선을 긋기 전에 지금 그으려는 곳의 왼쪽과 오른쪽에 가로선이 있으면 continue 해버리면 된다.
이 코드는 지금 그으려는 가로선 왼쪽끝의 왼쪽선, 오른쪽선과 / 가로선 오른쪽끝의 왼쪽선, 오른쪽선을 모두 체크해준다.
원래는 이렇게 했는데, 안돼서 도대체 왜 안되는지 많이 고민했다.
if (map[i][j] != 1 || map[i][j] != -1) continue;틀린 이유는, 이렇게 하면 지금 그으려는 가로선의 오른쪽에 가로선이 있을 경우를 놓치게 되기 때문이었다. 아래 방법대로 하면 안된다!
구현 방법
1. 라인마다 가로선이 홀수인지를 판단해서, 가로선이 홀수개인 라인이 > 3 이면 종료시킨다.
2. 사이즈별로 for문에 DFS를 돌린다 (최소 가로선을 구하는 문제이므로 가장 작은 사이즈인 0부터 돌린다)
pseudo code
boolean dfs (int x, int y,...) {
종료조건 {
if(지금 사다리가 조건을 충족하면) return true;
return false;
}
for (i : x~가로선을 그을 수 있는 범위인 H) {
for (j : y~세로선 개수인 N - 1) {
if (가로선을 그을 수 없다면) continue;
맵에 가로선 표시;
dfs(...);
맵에 가로선 지우기;
}
y = 0; //입력받은 y가 끝나면 다음 i턴에서는 0부터 시작해야 함!
}
}
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main {
private static int N, M, H, map[][];
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
H = Integer.parseInt(st.nextToken());
map = new int[H + 1][N];
for (int i = 0; i < M; i++) {
st = new StringTokenizer(br.readLine());
int a = Integer.parseInt(st.nextToken()) - 1;
int b = Integer.parseInt(st.nextToken()) - 1;
map[a][b] = 1;
map[a][b + 1] = -1;
}
if (searchOddNum() > 3) {
System.out.println("-1");
return;
} else {
for (int i = 0; i <= 3; i++)
if (dfs(0, 0, 0, i))
return;
}
System.out.println("-1");
}
private static boolean dfs(int x, int y, int cnt, int size) {
if (cnt == size) {
if (ladderCheck()) {
System.out.println(size);
return true;
}
return false;
}
for (int i = x; i < H; i++) {
for (int j = y; j < N - 1; j++) {
// if (map[i][j] != 1 || map[i][j] != -1) continue; 이건 안됨!
if (map[i][j] != 0 || map[i][j + 1] != 0) continue;
map[i][j] = 1;
map[i][j + 1] = -1;
if (dfs(i, j + 2, cnt + 1, size)) return true;
map[i][j] = 0;
map[i][j + 1] = 0;
}
y = 0;
}
return false;
}
private static boolean ladderCheck() {
for (int j = 0; j < N; j++) {
int nx = 0, ny = j;
while (nx <= H) {
if (map[nx][ny] == 1) ny++;
else if (map[nx][ny] == -1) ny--;
nx++;
}
if (ny != j) return false;
}
return true;
}
private static int searchOddNum() {
int oddNum = 0;
for (int j = 0; j < N - 1; j++) {
int num = 0;
for (int i = 0; i < H; i++)
if (map[i][j] == 1) num++;
if (num % 2 == 1) oddNum++;
}
return oddNum;
}
}
이전에 푼 방법
처음 풀었을 때 방법이 나름 마음에 들어서, 첨부하자면
1. 이 때는 사다리의 가로줄을 배열의 한 칸으로 받았다.
boolean[][] 배열을 이용해서 가로줄이 있을 경우 true, 없을 경우 false로 받았다.
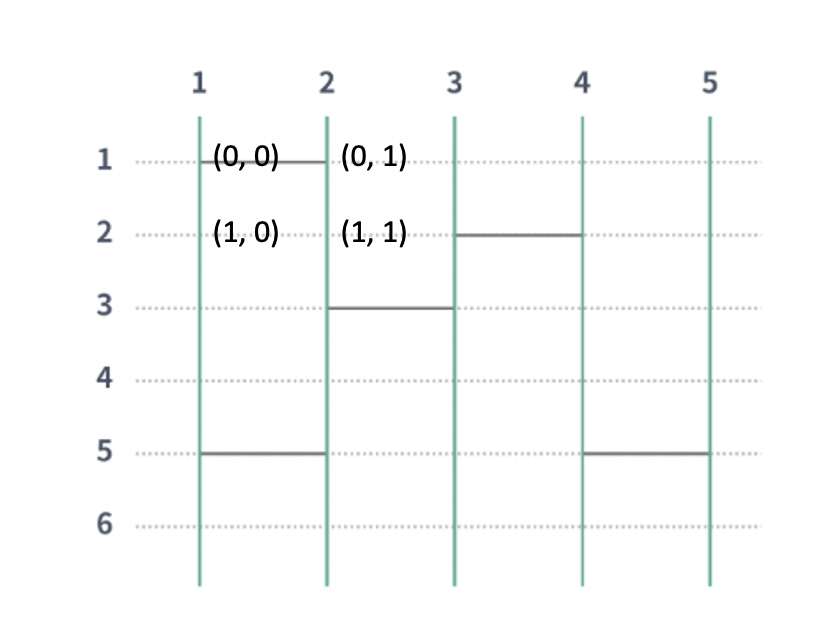
이 경우 map[0][0] = true, map[0][1] = false; 가 된다.
2. 전체적으로 DFS를 사용했다는 점과, 코드의 스타일은 비슷하다.
그런데 가로선을 그릴 수 있는지 판단하는 부분에서
boolean형을 활용했기에
if (오른쪽에 가로선이 이미 있는 경우) -> 오른쪽 칸과 오른쪽의 오른쪽칸은 못그리므로 3번째 오른쪽 칸으로 이동
else if (지금 내 칸에 가로선이 있는 경우) -> 2번째 오른쪽 칸으로 이동
else if (왼쪽에 가로선이 있는 경우) -> 지금 칸에는 그릴 수 없으므로 그 다음 칸으로 이동
else //내 왼쪽, 나, 내 오른쪽 모두에 없으면 그릴 수 있다는 뜻이므로
맵에 표시;
dfs(...);
맵에서 지워줌;

이렇게 구현했다.
나름 창의적? 인 방법으로 구현한 것 같아서 마음에 드는 코드였다.
이전에 푼 코드
import java.io.*;
import java.util.*;
public class Main {
static int n, m, h;
static boolean map[][];
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
n = stoi(st.nextToken());
m = stoi(st.nextToken());
h = stoi(st.nextToken());
map = new boolean[h + 2][n + 1];
for (int i = 0; i < m; i++) {
st = new StringTokenizer(br.readLine());
map[stoi(st.nextToken())][stoi(st.nextToken())] = true;
}
if(removeBranch()) { //가지치기
System.out.println("-1");
return;
}
arrangeLadder(1, 1, 0, 0);
arrangeLadder(1, 1, 0, 1);
arrangeLadder(1, 1, 0, 2);
arrangeLadder(1, 1, 0, 3);
System.out.println("-1");
}
private static boolean removeBranch() {
int cnt, totalCnt = 0;
for (int j = 1; j < n + 1; j++) {
cnt = 0;
for (int i = 1; i < h + 2; i++)
if (map[i][j]) cnt++;
if (cnt % 2 == 1) totalCnt++; //열마다 사다리 개수가 홀수개인 열의 개수를 센다
}
if (totalCnt > 3) return true;
else return false;
}
private static void arrangeLadder(int x, int y, int cnt, int size) {
if (cnt == size) {
if (ladder()) {
System.out.println(size);
System.exit(0);
}
return;
}
int j = y;
for (int i = x; i < h + 1; i++) {
while (j <= n - 1) {
if (map[i][j + 1]) j += 3;
else if (map[i][j]) j += 2;
else if (map[i][j - 1]) j++;
else { //나,좌우 모두 안칠해져있으면
map[i][j] = true;
arrangeLadder(i, j + 2, cnt + 1, size);
map[i][j] = false;
j++;
}
}
j = 1;
}
}
private static boolean ladder() {
int i, tempy;
for (int j = 1; j < n; j++) {
i = 0;
tempy = j;
while (i < h + 2) {
if (map[i][tempy - 1]) //왼쪽에 가로줄이 있다면 왼쪽으로 이동
tempy--;
else if (map[i][tempy]) //오른쪽에 가로줄이 있다면
tempy++;
i++;
}
if (tempy != j) return false;
}
return true;
}
public static int stoi(String str) {
return Integer.parseInt(str);
}
}


처음 풀었을때 내 코드가 가장 빨랐는데,
두번째 풀었을 때도 내 코드가 가장 빨라서 뭔가 신기했다.
좀 힘들긴 했지만 재미있는 문제였다.
끝!
'algorithm > Baekjoon' 카테고리의 다른 글
| [백준] 17143.낚시왕 (java) / 시뮬레이션 (0) | 2020.02.11 |
|---|---|
| [백준] 16637.괄호 추가하기 (java) / DFS, 백트래킹, 조합, 시뮬레이션 (0) | 2020.02.10 |
| [백준] 1647.도시분할계획 (java) / 크루스칼, Union-Find (0) | 2020.02.02 |
| [백준] 17472.다리 만들기 2 (java) / 크루스칼, Union-Find, DFS, BFS, 시뮬레이션 (0) | 2020.02.01 |
| [백준] 17244.아맞다우산 (java) / BFS, Permutation (0) | 2020.01.07 |




댓글